Tabela de conteúdos
2. Tutoriais de Funções Matemáticas no R
No nosso Tutorial 1a de introdução à linguagem, vimos alguns tipos básicos de informações que podem ser armazenados em objetos do R e a estrutura básica de armazenamento que são os vetores. Neste tutorial vamos apresentar algumas ferramentas de operações algébricas e estatísticas no R.
Criando Vetores
As características básica do vetor no R são:
- uma dimensão de dados
- tamanho definido pelo número de elementos
- armazena dado de um só tipo
- classificado pelo tipo de dado armazenado
Os vetores podem ser construídos de várias formas no R, as principais são:
Execute o código abaixo para entender como criar uma sequência de 1 a 10 em intervalos inteiros de diferentes maneiras:
a <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) b <- seq(from = 1, to = 10, by = 1) c <- 1:10 length(a) class(a) length(c) class(c) a == b a == c identical(a, b) identical(a, c)
Acima, apesar dos objetos conterem a mesma informação de dados, o objeto c pertence a classe
integer, representada por números inteiros, enquanto os outros objetos são da classe numeric. Os objetos armazenam a mesma coisa, mas não são idênticos já que o atributo de classe é diferente. Essa atribuição a classe é feita pelas funções ao criar os objetos.
Operações com Vetores
As operações algébricas com vetores apresentam duas características importantes: equivalência de posição e ciclagem do vetor de menor tamanho. A equivalência define que os valores serão operados respeitando suas posições equivalentes entre dois ou mais vetores de mesmo tamanho. No caso de vetores de tamanhos diferentes, há a ciclagem dos elementos do vetor de menor tamanho. Nesse último caso, se o vetor maior é múltiplo do menor, não há nenhuma mensagem na operação. Caso não possa ciclar todos os elementos o mesmo número de vezes, o R opera parte do vetor menor no último ciclo e avisa com uma mensagem de alerta: 'longer object length is not a multiple of shorter object length'.
Estude os resultados dos comandos nos três exemplos abaixo para entender as operações com vetores.
a <- 1:10 b <- -(1:10) a+b sum(a, b)
Aqui temos a característica da equivalência. Os vetores de mesmos tamanhos, quando operados algebricamente, operam os valores das posições equivalentes.
a <- seq(from = 0, to = 1, length = 9) b <- seq(from = 0, to = 0.5, length = 9) a b a/b b/a 1+b/a (1+b)/a
Nesse último bloco de código temos, além da equivalência entre as posições de vetores de mesmo tamanho, algumas operações algébricas que retornam palavras reservadas no R: NaN, Inf e -Inf:
O NaN significa 'not a number', ou seja um valor numérico indefinido ou irrepresentável. Operações como 0/0 ou √-1 retornam NaN. Dividir um número real por 0 retorna Inf ou -Inf1).
a <- rep( c(1, 2), each = 3 ) length(a) b <- rep( c(3, 4), 6) length(b) a+b
a <- rep( c(1, 2, 3), each = 3 ) length(a) b <- rep( c(3, 4), length = 7) length(b) a+b
Nestes blocos temos o princípio da ciclagem. Ao realizar operações com vetores de tamanhos diferentes, o vetor menor é ciclado, ou seja, reutilizado para a operação. Note que se o tamanho dos vetores for múltiplo, todas as posições do vetor serão utilizadas um mesmo número de vezes e o R não retorna nenhuma mensagem de aviso2). Se os vetores não forem múltiplos a operação é realizada porém com uma mensagem de aviso.
Operações sintéticas
As operações de vetores acima retornam vetores do tamanho do vetor operado, ou do maior vetor. Vamos ver algumas operações que retornam vetores de tamanhos distintos ou apenas um atributo do vetor. Para isso, vamos utilizar a seguinte informação de uma pessoa em dieta que anotou seu peso mensalmente durante um ano e obteve os valores:
pesos <- c(78.4, 79.8, 76.0, 75.3, 77.4, 78.6, 77.9, 78.8, 79.2, 75.2, 75.0, 79.4)
A diferença de peso entre um mês e o consecutivo é obtida pela função diff:
pesos.dif <- diff(pesos)
Que tem a particularidade de retornar como resultado um vetor de tamanho uma posição menor do que o comprimento do vetor de entrada.
length(pesos) length(pesos.dif)
Vamos calcular o valor mínimo, máximo e médio do peso:
max(pesos) min(pesos) mean(pesos)
O valor mínimo e máximo também é obtido com:
range(pesos)
E mesmo que não tivéssemos a função mean poderíamos calcular a média com:
sum(pesos)/length(pesos)
Vocabulário de Referência
Um dos problemas que enfrentamos ao aprender uma linguagem é a falta de vocabulário que nos impede de fazer uma comunicação eficiente. Isso acontece no R também. Além disso, é mais fácil encontrar um documento que explica como fazer uma análise complexa do que encontrar o nome de uma função que faz uma tarefa simples! É muito bom poder contar com um dicionário da linguagem nessas horas. No caso do R, e outras linguagens computacionais, é comum termos cartões de referência da linguagem. São, geralmente, poucas páginas contendo um vocabulário básico para se comunicar. Na imagem temos a página com as referências às funções matemáticas. Pode baixar o arquivo clicando na imagem do card ou no nosso material de apoio. É possível fazer quase tudo que precisamos no R com essas 4 páginas de vocabulário básico do card!! Imprima frente e verso e mantenha junto ao computador!
Operando NaN
Calcule a média do logaritmo na base 10 das diferenças de peso, obtidas no tópico anterior ("Operações sintéticas"):
mean(log(pesos.dif, base = 10))
Este comando retorna um aviso e um resultado não numérico, NaN, pois não existem logaritmos de números negativos3). NaN significa Not a Number, e serve para alertar que o usuário tentou realizar uma operação matemática não definida numericamente ou valores não pertencentes aos números reais.
pesos.dif log(pesos.dif, base = 10)
Operando Valores Faltantes
É muito comum termos posições em vetores que não tem informação disponível. Por exemplo, no caso acima a pessoa pode ter esquecido de anotar o peso em um dos meses. Nesses casos, para registrar que o valor não está disponível podemos usar a palavra reservada NA.
Basta um valor faltante (NA, que significa Not Available) ou não numérico (NaN) em um vetor para que operações numéricas retornem NA e NaN, respectivamente. Verifique:
faltaUm <- pesos faltaUm[5] <- NA faltaUm mean(faltaUm)
sqrt(-1:9) mean(sqrt(-1:9))
Muitas funções têm um argumento lógico na.rm que, se declarado verdadeiro, desconsidera os valores NA e NaN. Verifique:
mean(faltaUm, na.rm = TRUE) var(sqrt(-1:9), na.rm = TRUE)
Índice de Shannon
O índice de diversidade de Shannon é dado pela fórmula:
$$H´=-\sum \ p_i \ ln p_i$$
onde $p_i$ é a proporção de indivíduos da espécie $i$ em relação ao total de indivíduos. A seguir construímos um objeto chamado abund, que representa as abundâncias das espécies em uma comunidade. Em seguida, calculamos o valor do índice, usando objetos intermediários, sempre verificando cada passo intermediário para garantir que os objetos formados contém o valor que queremos:
abund <- c(13, 23, 29, 29, 30, 48, 72, 76, 83, 84, 86, 97, 102, 229, 343) tot <- sum(abund) tot pi <- abund/tot pi log.pi <- log(pi) log.pi pi.log.pi <- pi*log.pi pi.log.pi H <- - sum(pi.log.pi) H
O mesmo cálculo pode ser feito em uma única linha com:
-sum(abund/sum(abund) * log(abund/sum(abund)))
Compare os resultados.
Funções Aninhadas
No código acima, podemos observar uma característica muito básica e fundamental da sintaxe da linguagem R: o aninhamento de funções. O interpretador do R foi desenhado para ler a linha de comando começando pelas funções mais internas e expandindo o resultado para as mais externas, de maneira análoga com o que fizemos ao calcular o valor com os objetos intermediários. No caso do código aninhado, os valores intermediários só existem durante o processamento do código.
Onde foi parar o pi?
No tópico anterior criamos um objeto pi, mas este é nome que o R usa para armazenar o número π4)!!! ![]()
Mas não se preocupe. O objeto pi original pertence ao pacote base e continua lá.
Como o R busca qualquer objeto chamado na ordem estabelecida no caminho de busca (search path) e como o sua área de trabalho (workspace) está na frente do pacote base, ele irá usar o novo objeto pi se você digitar apenas o nome do objeto, pois este será o primeiro objeto com este nome que ele encontrará.
Verifique o caminho de busca (search path) com:
search()
Sua área de trabalho (workspace) tem o nome padrão .GlobalEnv e tem a precedência no caminho de busca de todos os outros compartimentos de memória (environments). Agora o objeto pi de seu workspace tem precedência ao objeto pi do pacote base.
pi
Podemos indicar para o R que queremos um objeto em um compartimento de memória específico e, nesse caso, ele irá buscar o objeto diretamente. Podemos então acessar o número π explicitando o ambiente (pacote) onde ele está da seguinte forma, compartimento::objeto, como a seguir:
base::pi
Nesse caso, se o objeto não existir nesse compartimento, mas estiver em outro, o R não irá considerá-lo e retornará a mensagem de erro que o objeto não foi encontrado. Veja o código a seguir:
a <- 0 base::a
Distribuições Probabilísticas
O R contém muitas distribuições probabilísticas no pacote stats, carregado automaticamente quando iniciamos uma sessão no R.
Vamos entender como essas distribuições são utilizadas no R com um exemplo de dados.
Eita avião apertado
 Um artigo reportou a largura do quadril de mulheres de cerca de vinte anos como sendo 5) 35 ± 3.4 cm (média e desvio padrão). Por outro lado, os assentos de aviões por padrão tem cerca de 40.6 cm 6) de largura. Com essas informações e algumas premissas podemos inferir muitas coisas. As premissas mais importantes são:
Um artigo reportou a largura do quadril de mulheres de cerca de vinte anos como sendo 5) 35 ± 3.4 cm (média e desvio padrão). Por outro lado, os assentos de aviões por padrão tem cerca de 40.6 cm 6) de largura. Com essas informações e algumas premissas podemos inferir muitas coisas. As premissas mais importantes são:
- a média e o desvio são uma boa estimativa dos parâmetros da distribuição da largura de quadril da população de mulheres de 20 e poucos anos;
- a distribuição de largura do quadril é bem representada por uma distribuição probabilística normal
A partir desses dois parâmetros (média e desvio) da distribuição normal podemos, por exemplo, simular os dados de uma amostra de 200 tamanhos de quadris no R. A função rnorm faz a simulação de amostras aleatórias de uma distribuição normal e tem como argumentos n que é o tamanho amostral, mean e sd, que são os parâmetros que definem a distribuição normal.
amostra <- rnorm(n = 200, mean = 35, sd = 3.4) hist(amostra)
Quantas mulheres na nossa amostra não caberiam nas cadeiras do avião?
sum(amostra > 40.6)
Conseguiu entender o que foi feito acima? Uma forma de compreender códigos mais complexos é dividir em partes e estudar cada elemento independentemente:
vf_41 <- amostra > 41 vf_41 sum(vf_41) # lembre-se que TRUE pode ser considerado como 1 e FALSE como 0.
Como entendemos todos os comandos acima, podemos refazer a simulação de amostra e contar as mulheres que não caberiam nos assentos de avião em uma única linha. Agora vamos repetir a nossa amostra 10x:
sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6) sum(rnorm(n = 200, mean = 35, sd = 3.4) > 40.6)
A cada amostra nosso valor varia um pouco. Isso ocorre porque a simulação de amostra é uma realização aleatória de 200 valores da distribuição normal teórica. Podemos obter o valor teórico dessa proporção de mulheres em nossa população estatística teórica. Para isso usamos a função pnorm que tem os parâmetros q de quantil e os parâmetros da normal:
pnorm(q = 40.6, mean = 35, sd = 3.4)
Esse valor é a proporção de mulheres que caberiam nos assentos com 40.6cm de largura. Para o cálculo das que não caberiam podemos fazer de duas formas:
1 - pnorm(q = 40.6, mean = 35, sd = 3.4) pnorm(q = 40.6, mean = 35, sd = 3.4, lower.tail = FALSE)
Por volta de 5% das mulheres não caberiam nessas poltronas, o que não parece lá muito simpático por parte das companhias aéreas!
Vamos nos perguntar outra coisa, por exemplo, qual o tamanho de assento no qual caberiam 99% das mulheres de cerca de vinte anos? Para extrair esse valor diretamente da distribuição normal teórica, usamos a função qnorm.
qnorm(p = 0.99, mean = 35, sd = 3.4)
Isso significa que apenas 2.3 cm de aumento na largura das poltronas das aeronaves é capaz de reduzir em 5x a proporção de mulheres que não caberiam. Parece uma boa política para a companhia aérea…
Amplitude de uma Amostra Normal
Vamos simular uma amostra de 10 valores, tomados de uma distribuição normal com média 10 e desvio padrão 2.5:
normal.1 <- rnorm(10, mean = 10, sd = 2.5)
Calcule mínimo e máximo e a amplitude destes valores:
range(normal.1) diff(range(normal.1))
O que acontece à medida que aumentamos o tamanho da amostra? Verifique para simulações de 100, 1000 e 10000 valores:
diff(range(rnorm(100, mean = 10, sd = 2.5))) diff(range(rnorm(1000, mean = 10, sd = 2.5))) diff(range( rnorm(10000, mean = 10, sd = 2.5)))
As Funções que operam distribuições de probabilidades
O que foi apresentado para Distribuição Normal pode ser generalizado para outras distribuições de probabilidade.
Há quatro principais funções para se extrair informações básicas de distribuições probabilísticas:
- ddistrib - retorna a densidade probabilística para um dado valor da variável;
- pdistrib - retorna a probabilidade acumulada para um dado valor da variável;
- qdistrib - retorna o quantil para um dado valor de probabilidade acumulada;
- rdistrib - retorna valores (números aleatórios) gerados a partir da distribuição;
No caso da Distribuição Normal: distrib = norm. Para outras distribuições temos:
DISTRIBUIÇÕES ESTATÍSTICAS NO R
| Distribuição | Nome no R | Parâmetros7) |
|---|---|---|
| beta | beta | shape1, shape2, ncp |
| binomial | binom | size, prob |
| Cauchy | cauchy | location, scale |
| qui-quadrado | chisq | df, ncp |
| exponential | exp | rate |
| F | f | df1, df2, ncp |
| gamma | gamma | shape, scale |
| geométrica | geom | prob |
| hypergeométrica | hyper | m, n, k |
| log-normal | lnorm | meanlog, sdlog |
| logística | logis | location, scale |
| binomial negativa | nbinom | size, prob |
| normal | norm | mean, sd |
| Poisson | pois | lambda |
| t de Student | t | df, ncp |
| uniforme | unif | min, max |
| Weibull | weibull | shape, scale |
| Wilcoxon | wilcox | m, n |
Qui-quadrado na unha
Vamos fechar com um exemplo hipotético de um estudo de preferência alimentar. Nosso ecólogo virtual estimou a proporção de cinco tipos de itens alimentares para uma espécie de ave em uma área. Esses itens estavam disponíveis na proporção de 60%, 28%, 9%, 2,5% e 0,5%. No mesmo local, amostrou-se ao acaso eventos de alimentação desta ave, contando quantos eventos foram de consumo de cada um dos itens. Os resultados das contagens dos eventos de alimentação foram 544, 285, 117, 54, 12, para cada um dos itens respectivamente.
Vamos criar os objetos com estes valores:
disp <- c(60, 28, 9, 2.5, 0.5) cons <- c(544, 285, 117, 54, 12)
A pergunta que esses trabalhos de dieta se fazem é: “a espécie tem preferência por algum item?”. Se isso não acontecer, espera-se que 60% do total de itens consumidos sejam do primeiro tipo, e assim por diante. O total de itens consumidos é:
totItens <- sum(cons)
E os valores esperados pela hipótese de falta de preferência serão:
espe <- totItens*disp/100
O que resulta em uma série de desvios entre os valores esperados e os observados:
desv <- cons - espe desv
Para testar esta diferença, calculamos o valor do Qui-quadrado, que é a somatória de cada desvio elevado ao quadrado e dividido pelo respectivo valor esperado:
dQuad <- desv^2/espe dQuad qui2 <- sum(dQuad) qui2
Qual a chance de um valor de Qui-quadrado maior ou igual a este ocorrer por acaso (ou seja, mesmo que não haja preferência)? Como são cinco itens alimentares, temos quatro graus de liberdade, e o que queremos saber é: qual a probabilidade de encontrarmos a diferença observada em relação ao esperado ou maiores, em um cenário onde a espécie não tem preferência alimentar (hipótese nula). Obtemos isto com a função de probabilidade acumulada da distribuição de Qui-quadrado:
pchisq(q = qui2, df = 4, lower.tail = FALSE)
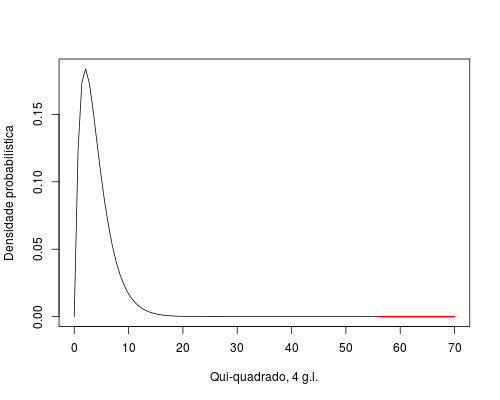
A probabilidade é baixíssima, o que indica que o consumo não foi na proporção da disponibilidade dos itens alimentares. Usamos o argumento lower.tail = FALSE para que a função retorne a probabilidade da parte que resta da distribuição, após este valor8), que está representado em vermelho na figura abaixo:
Extra
Para reproduzir a figura acima digite os comandos abaixo. Para entender, veja a ajuda da função curve.
## Faz o grafico da funcao Qui-quadrado com 4 graus de liberdade, ## veja a ajuda da funcao curve curve(dchisq(x, df = 4), 0, 70, xlab = "Qui-quadrado, 4 g.l.", ylab = "Densidade probabilística") ## Sobrepoe uma linha vermelha a partir ##do valor calculado do Qui-quadrado curve(dchisq(x, df = 4), 56.93, 70, add = T, col = "red", lwd = 2)
Código Canalizado
As linguagens de programação, assim como as linguagens naturais, estão em constante modificação. Existe na comunidade do R um movimento com um novo dialeto que foi chamado de tidyverse. Esse conjunto de pacotes propõem formas mais compactas de códigos para manipular e grafar dados9). Este curso é baseado na forma mais original da linguagem contida nos pacotes básicos da distribuição do R e sem a pretensão de ensinar esse novo dialeto. Entretanto, irão encontrar muita documentação que usa essa filosofia. Uma das dificuldades para entender o código nesse dialeto é a introdução do conceito de canalização de procedimentos, onde o resultado de uma função pode ser direcionada a outra através do pipe (%>%). Essa ferramenta, que está no pacote magrittr, modifica bastante a lógica de funções aninhadas do interpretador do R. Abaixo listamos alguns dos conceitos básicos para entender os códigos em tidyverse:
x %>% fé equivalente af(x)x %>% f(y)é equivalente af(x, y)x %>% f %>% g %>% hé equivalente ah(g(f(x)))x %>% f(y, .)é equivalente af(y, x)x %>% f(y, z = .)é equivalente af(y, z = x)