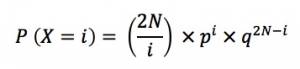Carol Mendonça
Sou bióloga, graduada como bacharela pelo Instituto de Biociências (USP) e licenciada pela Faculdade de Educação (USP). Possuo grande interesse na área de Genética, especialmente em Biologia Molecular. Trabalho desde 2013 no Laboratório Nacional de Células-Tronco Embrionárias, a cargo da Profa. Dra. Lygia da Veiga Pereira, no grupo que pesquisa Síndrome de Marfan. Atualmente, tenho intenção de fazer pós-graduação no Laboratório de Drosofilídeos sob orientação da Profa. Maria Vibranovski, cuja principal linha de pesquisa é a evolução genômica. Além disso, tenho grande apreço pela educação em Ciências, tendo participado de diversos projetos de extensão universitária e atuado como professora em cursinhos populares.
I. Meus exercícios
II. Trabalho final
II.I Plano A: Uma simulação da deriva genética
Contextualização
A deriva genética é uma das quatro forças evolutivas e pode ser definida como: mudanças aleatórias nas frequências alélicas de uma população (RIDLEY, 2006). Considerando apenas a ação da deriva genética, para um gene bialélico, as probabilidades das frequências alélicas na geração seguinte podem ser calculadas pelo uso da distribuição binomial. Este é o Modelo Wright-Fischer que tem as seguintes premissas: (1) uma população de N indivíduos tem 2N alelos; (2) a próxima geração terá 2N alelos, sorteados ao acaso dentre os milhões de gametas produzidos na geração anterior; (3) todos os gametas têm chance idêntica de serem sorteados (não há seleção); (4) não há mutação ou migração e os cruzamentos se dão ao acaso (MEYER, 2016).
Alternativamente à solução analítica, a probabilidade de um alelo se manter na população com determinada frequência pode ser estimada por meio de simulações. Para esta estimativa, é necessário levar em consideração: o número de indivíduos na população, o número de gerações, a frequência inicial do alelo e o número de populações a serem simuladas. Com estes parâmetros, a função proposta realizaria as simulações, apresentando no final: um gráfico com as trajetórias individuais de cada população, um histograma com as frequências finais nas populações e o p-valor. Em outras palavras, ela responderia a pergunta: “Qual é a probabilidade que após n gerações em X populações de tamanho N, a frequência do alelo A (gene bialélico) seja Y?”.
Planejamento da função
Entrada: deriva (N, gen, f, pop, teste)
N= tamanho de cada população (classe: integer,N> 0).gen= número de gerações a ser simulado (classe: integer,gen> 0).f= frequência do alelo A (classe: numeric com 2 casas decimais, 0 ≤f≤ 1).pop= número de populações (classe: integer,pop> 0).teste= frequência final de alelos a ser testada (classe: numeric com 2 casas decimais, 0 ≤teste≤ 1).
Verificando os parâmetros:
Né um número inteiro e maior que 0? Se não, escreve: “N precisa ser um numero inteiro e > 0.”gené um número inteiro e maior que 0? Se não, escreve: “gen precisa ser um numero inteiro e > 0.”fé ≥ 0 e ≤ 1? Se não, escreve: “f deve estar no intervalo 0 ≤ f ≤ 1.”popé um número inteiro e maior que 0? Se não, escreve: “pop precisa ser um numero inteiro e > 0.”testeé ≥ 0 e ≤ 1? Se não, escreve: “teste deve estar no intervalo 0 ≤ f ≤ 1.”
Pseudo-código:
- Cria objeto
simulacaocomNNAs. - Cria objeto
f.finalcompopNAs. - Cria objeto
populacaocomf×Ncaracteres “A” e 1 - (f×N) caracteres “a”. - Plota área para gráfico com eixo-X entre 0 -
gene eixo-Y entre 0 - 1. - Entra em um ciclo
forcom contadorjde 1 atépop.- Entra em um ciclo
forcom contadoride 1 atégen.- Amostra com reposição
Nalelos depopulacaoe guarda emsimulacao. - Conta numero de “A”, divide por
Ne guarda emfA. - Plota coordenada
i,fAno grafico. - Copia
simulacaoempopulacao. - Zera
simulacaopreenchendo-no comNNAs.
- Une os pontos no grafico.
- Preenche posição
jdef.finalcomf.A. - Redefini
populacaocomf×Ncaracteres “A” e 1 -f×Ncaracteres “a”. - Zera
simulacaopreenchendo-no comNNAs.
- Cria histograma de
f.finalcom linha vertical emteste. - Calcula o p-valor dividindo o número de vezes em que
f.final==testee dividindo porpop.
Saída:
- Histograma com a distribuição das frequências alélicas finais das populações.
- Gráfico de dispersão com as trajetórias individuais de cada uma das populações.
- O p-valor: probabilidade de uma determinada frequência (
teste) ao final das simulações.
A função parece bem clara. Na verdade o próprio pseudo-código dela já é quase que a função terminada. Se quiser, pode seguir essa proposta. OBS: cuidado com códigos desnecessários ou redundantes: será que é memso necessário unir os pontos do gráfico? É necessário “zerar” os vetores antes do próximo ciclo?
II.II Plano B: Jogo dos Micos
Contextualização
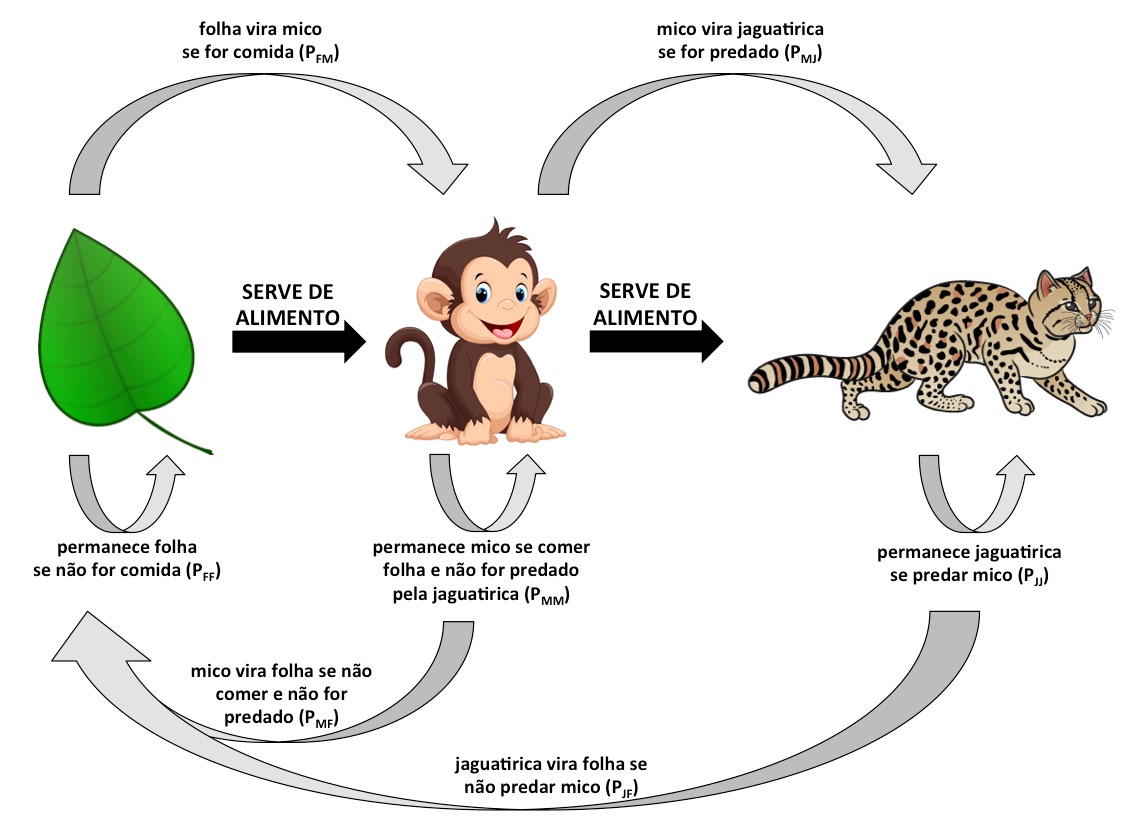
A Estação Biologia (http://www.ib.usp.br/estacaobiologia/) é um projeto de extensão universitária do Instituto de Biociências da USP que tem como principal objetivo a recepção de visitas escolares. Uma das atividades que é oferecida para os visitantes é o Jogo dos Micos, que foi desenvolvido com base em uma atividade de dramatização de presa e predador. Os alunos são divididos em três grupos (plantas, micos e jaguatiricas) e o jogo consiste em várias rodadas de pega-pega. Em cada uma delas, os micos tentam comer as plantas e as jaguatiricas os micos. Ao término da rodada, os papéis são redistribuídos como é ilustrado na figura abaixo.
O principal objetivo da atividade é mostrar a robustez da comunidade, isto é: mesmo que as crianças tenham trocado de papel ao longo do jogo, as três classes de espécie ainda permanecem. Para enfatizar a importância de cada uma das espécies, pode ser feita uma rodada extra em que uma das classes não está presente. Por exemplo: se as plantas não participarem, os micos serão todos predados e virarão jaguatiricas. Na próxima rodada, faltará alimento para as jaguatiricas e todas acabarão virando planta. A dúvida em relação à atividade é a proporção das classes que maximize a permanência de todas elas no jogo. Em outras palavras: “Dado um número X de crianças, quantas devem estar em cada classe de forma que todas as classes permaneçam no jogo por mais tempo?”.
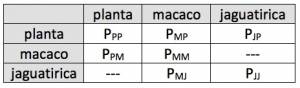
Para responder essa pergunta, é necessário levar em consideração a probabilidade de transição ou de permanência em cada uma das classes. Para estimá-las, seriam feitas medidas empíricas durante o jogo, levando em consideração as possíveis diferenças entre meninas e meninos. Assim, na matriz de transição mostrada abaixo, cada uma das probabilidade é na verdade uma somatória de 4 probabilidades: p(menina pegar menina), p(menina pegar menino), p(menino pegar menino) e p(menino pegar menina). A função proposta receberia o número de crianças presentes e faria simulações para determinar quantas devem ser alocadas em cada classe para que o jogo dure mais tempo. Para isso, seriam feitas multiplicações sucessivas de matrizes até que uma das classes não esteja mais presente.
Planejamento da função
Entrada: micos (N, meninas)
N= número de crianças (classe: integer,N> 0).meninas= número de meninas (classe: integer,meninas≥ 0).
Verificando os parâmetros:
Né um número inteiro e maior que 0? Se não, escreve: “N precisa ser um numero inteiro e > 0.”meninasé um número inteiro e ≥ 0? Se não, escreve: “meninas precisa ser um numero inteiro e ≥ 0.”
Pseudo-código:
- Distribui
meninasno data frameprop.meninascom todas as permutações possíveis. - Faz uma cópia de
prop.meninasemgirls. - Cria data.frame
girls.copiacom as mesmas dimensões degirlspreenchido com NAs. - Distribui
N-meninasno data frameprop.meninoscom todas as permutações possíveis. - Faz uma cópia de
prop.meninosemboys - Cria data.frame
boys.copiacom as mesmas dimensões deboyspreenchido com NAs. - Entra em um ciclo
whileaté que, em todas os casos, pelo menos uma das três classes não esteja mais presente.- Multiplica cada uma das linhas de
girlspormt.girls(matriz de transição das meninas). - Guarda o resultado da multiplicação de matrizes em
girls.copia. - Copia
girls.copiaemgirlse zeragirls.copiapreenchendo-no com NAs. - Multiplica cada uma das linhas de
boyspormt.boys(matriz de transição dos meninos). - Guarda o resultado da multiplicação de matrizes em
boys.copia. - Copia
boys.copiaemboyse zeraboys.copiapreenchendo-no com NAs.
- Seleciona o caso dentre
girls.copiaeboys.copiaque manteve as 3 classes por mais tempo no jogo. - Recupera em
prop.meninasouprop.meninosa permutação inicial associada ao caso selecionado. - Calcula as proporções do segundo gênero com base no caso selecionado.
Saída:
- Data frame com o número de meninas e meninos em cada uma das classes (plantas, micos e jaguatiricas).
Essa função parece desafiadora, mas você tbm parece preparada. Se você esta confortável com o método acho que é ok você seguir em frente nesta proposta tbm, caso queira.
Se quiser conversar mais sobre as funções (ou pedir conselhos, dicas etc) é só escrever aqui que pretendo revisar esta página dia 09/06 antes das 12hrs. Ou me mandar uma mensagem por whatsapp (11) 9-9199-3842.
Twister (ou Matheus Januario)
II.III Referências
MEYER, D. Deriva genética, 2017.
RIDLEY, M. Evolution. Oxford: Blackwell Science Ltd, 2006. 752 p.
II.IV Links para o trabalho final
Para o trabalho final, resolvi seguir com o plano A. Como já explicado, a função tem como finalidade simular a deriva genética. Adicionalmente, fiz também uma função que simula as mudanças nas frequências alélicas por ação da seleção natural. Assim, como produto final, criei a função evol com a qual o usuário pode simular um modelo de deriva genética ou determinístico.