Índice
- O Curso R
-
- Tutoriais
-
- Apostila
-
- 6. Testes de Hipótese (em preparação!)
- Exercícios
-
- Material de Apoio
-
- Área dos Alunos
-
- Cursos Anteriores
-
IBUSP
Outras Insitutições
Linques
Visitantes
Outras Insitutições
Aluna de doutorado do Departamento de Genética e Biologia Evolutiva do IB-USP, sob orientação da profa Dra Lygia da Veiga Pereira.
O objetivo do meu projeto é investigar os mecanismos moleculares dos fenótipos cardiovasculares da Síndrome de Marfan, uma doença monogênica causada por mutações na proteína de matriz extracelular fibrilina-1. Também tenho interese em estudar o papel das fibrilinas durante o desenvolvimento do sistema cardiovascular humano, analisando a dinâmica de expressão de seus respectivos genes.
Link para os meus exercícios resolvidos: Meus Exercícios
A produção de cerveja normalmente envolve cinco etapas básicas: a brassagem, a fervura, a fermentação, a maturação e a carbonatação/refermentação. Durante a etapa de brassagem, os grãos de malte moído são cozidos em água a uma temperatura específica (normalmente entre 60-70 °C) que propicie a atuação ótima de enzimas que degradam o amido presente nos grãos, convertendo-os em açúcares menores. O extrato obtido ao final desta etapa é chamado de mosto e contém os açúcares a serem utilizados pela levedura na produção de álcoois. A etapa de fervura consiste no cozimento do mosto a 100 °C. Durante esta fase, ocorre sua esterilização e concentração, além da caramelização dos açúcares e da evaporação de substâncias indesejáveis. Um outro evento muito importante que também ocorre normalmente durante a fervura é a lupulagem, que consiste na extração dos sabores e aromas da chamada “alma da cerveja”, o lúpulo, que fornece o amargor característico da bebida devido à isomerização de seus alfa-ácidos em altas temperaturas. Ao final deste processo, o mosto, agora mais complexo, é resfriado e sofre a inoculação de leveduras que serão responsáveis pela etapa seguinte, a fermentação, em que os açúcares são convertidos em álcoois (principalmente o etanol) e CO2.
A concentração de açúcares presente no mosto após a fervura vai determinar o grau alcoólico do produto final e também o chamado “corpo” da cerveja. A densidade do mosto pode e deve ser medida durante várias das etapas de produção, sendo as mais importantes após a fervura, e após a fermentação. Mais comumente entre os cervejeiros caseiros, mede-se a densidade do mosto em relação à densidade da água, chamada de gravidade específica (SG) ou densidade específica. Este valor, sem unidade, é obtido utilizando-se instrumentos de medição como o densímetro. O valor de densidade específica obtido após a fervura é chamado gravidade original (OG) e o obtido após a fermentação é chamado gravidade final (FG), e variam dependendo do tipo de cerveja.
A relação entre a OG e a FG é utilizada para o cálculo do “álcool por volume”, ou ABV, que é a concentração alcoólica final da cerveja, segundo a fórmula:
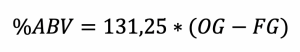 Desta forma, percebe-se a importância de se atingir o valor da OG desejável para o tipo de cerveja produzido, visto que dele dependem as características finais da bebida. Durante a produção, pode-se corrigir a gravidade específica aumentando-se o tempo de fervura, de forma a tornar o mosto mais denso (quando a OG está baixa) ou adicionando-se mais água após a fervura, diluindo-se o mosto (quando a OG está alta).
Desta forma, percebe-se a importância de se atingir o valor da OG desejável para o tipo de cerveja produzido, visto que dele dependem as características finais da bebida. Durante a produção, pode-se corrigir a gravidade específica aumentando-se o tempo de fervura, de forma a tornar o mosto mais denso (quando a OG está baixa) ou adicionando-se mais água após a fervura, diluindo-se o mosto (quando a OG está alta).
A função irá calcular o volume de água (em litros) ou o tempo adicional de fervura necessário para se corrigir a gravidade específica (SG) obtida, de forma a se alcançar a gravidade original (OG) desejada. De modo opcional, a função também calculará o índice de amargor (IBU) da bebida após a fervura, utilizando informações a respeito do(s) lúpulo(s) utilizado(s) fornecidas pelo usuário.
Entrada: brewtool (SG, OG, t.mosto, t.cal, vol, tempo.f, IBU, input)
SG = gravidade específica pós-fervura (OG) obtida pelo usuário por medida com densímetro (classe: numeric, com 3 casas decimais, 1.020 < SG < 1.120)OG = gravidade original desejada (classe: numeric, com 3 casas decimais, 1.020 < OG < 1.120)t.mosto = temperatura do mosto, em graus Celsius, no momento da medida de SG (classe: numeric, 0 < t.mosto < 85)t.cal = temperatura de calibração do densímetro utilizado, em graus Celsius (classe = numeric, t.cal > 0, default = 20)vol = vetor contendo os volumes do mosto antes e após a fervura, em litros (classe: numeric, vol[i] > 0)tempo.f = tempo de fervura, em minutos (classe: numeric, tempo.f > 0, default = 60)IBU = opção para o cálculo do índice de amargor (IBU) (classe: logic, default = FALSE)input = tabela de dados contendo as informações - peso (em gramas), tempo (em minutos pós início da fervura) e % de alfa-ácidos - do(s) lúpulo(s) utilizado(s), necessária apenas se IBU = TRUE (classe = data frame)Verificação dos parâmetros:
SG maior que 1.020 e menor que 1.120? Se não, stop(“SG fora do intervalo permitido, 1.020 < SG < 1.120”)OG maior que 1.020 e menor que 1.120? Se não, stop(“OG fora do intervalo permitido, 1.020 < OG < 1.120”)SG é um número com 3 casas decimais? Se não, warning(“SG deve ser um número com 3 casas decimais. O valor digitado foi ajustado para 3 casas.”)OG um número com 3 casas decimais? Se não, warning(“OG deve ser um número com 3 casas decimais. O valor digitado foi ajustado para 3 casas.”)t.mosto é um número inteiro entre 0 e 85? Se não, stop(“t.mosto deve ser um número inteiro entre 0 e 85”)t.cal é um número inteiro maior que 0? Se não, stop(“t.cal deve ser um número inteiro > 0”)vol[i] é um número maior que 0? Se não, stop(“vol deve conter apenas números > 0”)vol[1] menor que vol[2]? Se sim, warning(“Volume pré-fervura menor que o volume pós-fervura. A taxa de evaporação não poderá ser calculada. Verifique a ordem dos elementos do vetor (vol = c(pré, pós)).”)tempo.f é um número inteiro maior que 0? Se não, stop(“tempo.f deve ser um número inteiro > 0”)IBU = TRUE, input é um data frame contendo colunas de mesmo tamanho nomeadas “peso”, “tempo”, e “aa”? Se não, stop(paste(“As informações de”, input, “não estão corretas. Verifique a nomenclatura e o tamanho das colunas”.)) Pseudo-código:
SG formatando seu valor para 3 casas decimaisOG formatando seu valor para 3 casas decimaisSG.cal corrigindo a SG pela temperatura de calibração (t.cal)SG.dig com os 2 últimos dígitos de SG.calOG.dig com os 2 últimos dígitos de OGSG.pre com o cálculo do valor de SG pré-fervura dif subtraindo SG de OG –> dif = OG - SG.caldifdif = 0print.og = print(paste(“Sua OG”, (SG.cal), “já é igual à OG desejada, nada precisa ser feito. Prossiga com a receita.”, \n))a.acidos, contendo as informações de utilização dos alfa-ácidos para cada valor de SG pré-fervura de acordo com o tempo de fervura;IBU.tot = rep(NA, nrow(input))IBU.tot) para calcular o IBU de cada lúpuloU, contendo a % de utilização de alfa-ácidos para SG.pre correspondente ao tempo.f - input$tempo[i], de acordo com o data frame a.acidosa.acidos e armazenar seu valor em IBU.tot[i]print.ibu = print(paste(“Seu IBU é igual a”, sum(IBU.tot,), “.”))print.og e print.ibudif < 0v.final com o cálculo do volume final de mosto necessário para que SG.cal se iguale a OG –> v.final = (SG.dig*vol[2]/OG.dig)v.adic com o cálculo do volume a ser adicionado para o ajusteprint.og = print(paste(“Sua OG é igual a”, SG.cal, “. Para ajustá-la para”, OG, “adicione”, v.adic, “litros de água esterilizada.”, \n))a.acidos, contendo as informações de utilização dos alfa-ácidos para cada valor de SG pré-fervura de acordo com o tempo de fervura;IBU.pre = rep(NA, nrow(input))IBU.pos = rep(NA, nrow(input))IBU.pre) para calcular o IBU de cada lúpuloa.acidos e usando o volume atual (vol[2]). Armazenar seu valor em IBU.pre[i]a.acidos e usando o novo volume (v.final). Armazenar seu valor em IBU.pos[i]print.ibu = print(paste(“Seu IBU atual é igual a”, sum(IBU.pre,), “e seu IBU após o ajuste da OG será igual a”, sum(IBU.pos), “.”)print.og e print.ibudif > 0vol[1] ⇐ vol[2]print.og = print(paste(“Sua OG é igual a”, SG.cal, “. Como não foi possível calcular a taxa de evaporação, não será possível ajustá-la para”, OG, “.”, \n))vol[1] > vol[2] (else)evap com o cálculo da taxa de evaporação de líquido por minuto de fervura –> evap = abs(diff(vol))/tempo.fv.final com o volume final em que SG.cal é igual a OGv.evap com o cálculo do volume necessário de evaporação –> v.evap = vol[2] - v.finaltempo com o cálculo do tempo necessário para evaporação de v.evap –> tempo = v.evap/evapprint.og = print(paste(“Sua OG é igual a”, SG.cal, “. Para ajustá-la para”, OG, “ferva o mosto por mais”, tempo, “minutos.”))a.acidos, contendo as informações de utilização dos alfa-ácidos para cada valor de SG pré-fervura de acordo com o tempo de fervura;IBU.pre = rep(NA, nrow(input))IBU.pos = rep(NA, nrow(input))IBU.pre) para calcular o IBU de cada lúpuloU, contendo a % de utilização de alfa-ácidos para SG.pre correspondente ao tempo.f - input$tempo[i], de acordo com o data frame a.acidosa.acidos e usando o volume atual (vol[2]). Armazenar seu valor em IBU.pre[i]v.final = TRUEU, contendo a % de utilização de alfa-ácidos para SG.pre correspondente ao tempo.f - input$tempo[i] + tempo, de acordo com o data frame a.acidosa.acidos e usando o novo volume (v.final). Armazenar seu valor em IBU.pos[i]print.ibu.pos = print(paste(“Seu IBU após o ajuste da OG será igual a”, sum(IBU.pos), “.”)print.og, print.ibu e print.ibu.posSaída:
SG.cal)SG.cal para OG (v.adic), se SG.cal > OGtempo), se SG.cal < OGSG.cal para a OG.Julia Barreto
Entendo pouco da produção de cerveja mas vou tentar sugerir possibilidades. Uma seria a gente pensar numa demanda maior, tipo uma certa cervejaria interessada em produzir diferentes tipos de cerveja para um festival. Dessa forma, poderia entrar com um data-frame que contivesse diferentes valores de SG e OG para mais de uma cerveja produzida simultaneamente. Outra ideia seria também pensar na produção de diferentes tipos de cerveja amargor diferente. Tentando incluir mais variáveis que podem ser calculadas juntas ou uma em conseguencia da outra.
Me escreve se quiser conversar sobre essas ou outras ideias que venha a ter. Estou à disposição ![]() Julia Barreto
Julia Barreto
Oi Juliana,
Concordo com a Júlia. A ideéia é muito legal e vc. fez um bom trabalho na descrição e no pseudo-código. Já há algum controle de fluxo previsto com if, mas ficaria muito legal se incluisse alguma complexidade que necessitasse de um for. Uma possibilidade e ir pelo caminho sugerido pela Julia, criando a possibilidade do usuário poder definir mais de uma meta de OG desejada. Dessa forma, o usuário poderia tomar a decisão de qual caminho tomar (quanto de agua ou tempo de fervura) para diferentes metas de OG. Colocando isso em um loop, o desafio de programação ficaria mais completo. Avalie se faz sentido no contexto da sua ideia…
Juliana
Blog Homini Lúpulo: https://www.hominilupulo.com.br/
Em pesquisas em que a cultura de células é necessária, a contagem destas é crucial para a equiparação dos parâmetros iniciais do experimento, de forma a se poder comparar diferentes condições e diferentes eventos experimentais. Existem diferentes equipamentos, de diversas marcas, que efetuam a contagem automática de células, porém, o instrumento ainda mais utilizado em grande parte dos laboratórios é o hemocitômetro, muito conhecido como câmara de Neubauer. Esta câmara contém uma malha de leitura, que consiste em um desenho de linhas igualmente espaçadas, organizadas em quadrantes e com dimensões conhecidas, como ilustrado abaixo:
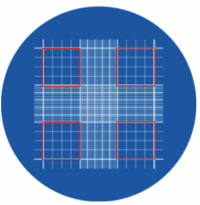 Figura 1. Esquema demonstrando a malha de leitura da câmara de Neubauer. Os quadrantes laterais, marcados em vermelho, são os mais comumente utilizados para contagem de células grandes. (Modificado de https://kasvi.com.br/como-e-realizada-contagem-de-celulas/)
Figura 1. Esquema demonstrando a malha de leitura da câmara de Neubauer. Os quadrantes laterais, marcados em vermelho, são os mais comumente utilizados para contagem de células grandes. (Modificado de https://kasvi.com.br/como-e-realizada-contagem-de-celulas/)
Quando uma solução de células em suspensão é aplicada à câmara, estas se espalham em camada única, distribuindo-se sobre as linhas. As células dispostas nos quadrantes de medida 4×4 (em vermelho na figura acima) são então contadas e a média, calculada. Este valor pode então ser multiplicado pelo fator 10.000, que foi obtido considerando-se a área do quadrante e sua profundidade na câmara, obtendo-se assim, a concentração de células por mililitro (ml). Caso a solução aplicada tenha sido diluída, o valor obtido deve ser multiplicado pela diluição. Desta forma, a fórmula para o cálculo pode ser resumida em:
 Obtendo-se este valor, é possível então calcular o volume necessário para se diluir a solução à concentração de células desejada (final) para o experimento:
Obtendo-se este valor, é possível então calcular o volume necessário para se diluir a solução à concentração de células desejada (final) para o experimento:
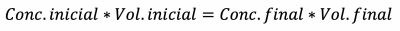
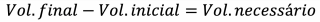
A função irá calcular a concentração da solução de células a partir da contagem obtida pelo usuário na câmara de Neubauer e também o volume necessário a ser adicionado à solução para ajuste desta concentração a uma concentração específica, também fornecida pelo usuário.
Entrada: neubauer (q, dil, vol, conc.f)
q = vetor de tamanho n contendo os valores obtidos de contagem para n quadrantes da câmara de Neubauer (classe = numeric, q = (c(q1 … qn)), sendo cada elemento >= 0)dil = fator de diluição (classe = numeric, dil > 0, default = 1)vol = volume da solução de células, em ml (classe = numeric, vol > 0)conc.f = concentração final de células desejada por ml (classe = numeric, conc.f > 0)Verificação dos parâmetros:
q é um vetor contendo apenas números inteiros maiores ou iguais a 0? Se não, stop(“Os valores de q devem ser números inteiros >= 0.”)dil é um número inteiro maior que 0? Se não, stop(“O fator de diluição dil deve ser um número inteiro > 0.”)vol é um número maior que 0? Se não, stop(“vol deve ser um número > 0.”)conc.f é um número maior que 0? Se não, stop(“conc.f deve ser um número > 0.”)Pseudo-código:
tam.q contendo o tamanho do vetor qsoma.q contendo a soma dos valores de qconc.i contendo a concentração inicial de célulastotal contendo a quantidade total de células na soluçãovol.adic contendo o volume necessário a ser adicionado para o ajuste de conc.i a conc.fconc.i –> print(paste(“A concentração da sua solução é de”, conc.i, “células/ml.”))total –> print(paste(“O total de células na sua solução é”, total,“.”))vol.adic –> print(paste(“O volume a ser adicionado à solução para a concentração de”, conc.f, “células/ml é de”, vol.adic, “ml.”))Saída:
conc.i)total)vol.adic)Julia Barreto
Como sugerido, decidi prosseguir com o plano A, adicionando o cálculo do índice de amargor (IBU) à função brewtool. Como explicado anteriormente, a função tem como objetivo auxiliar produtores caseiros no preparo da cerveja artesanal, indicando o valor de gravidade original (OG) obtido e as ações a serem tomadas para sua correção, quando necessário. De modo opcional, a função também calcula o IBU da cerveja antes e depois do ajuste da OG.